 |
 |
 |
 |
| zurück | |
|
|
|
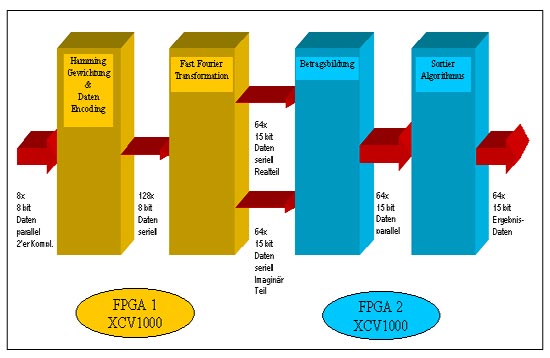 Schematisches Blockschaltbild |
|
|
Die FPGAs wurden entwickelt mit der Hardware-Beschreibungssprache VHDL. Außerdem fand der Xilinx Core Generator intensive Anwendung. Die Synthese erfolgte mit einem gängigen Synthesetool. Im Backend Flow kam insbesondere der Xilinx Floorplanner zum Einsatz, ohne den die Komponenten im zu 98% LUT-ausgelasteten Baustein nicht mehr platziert hätten werden können. Realisierung in VHDL In der Praxis bedeutet Hamming-Gewichtung die Multiplikation sämtlicher
Spektralwerte mit unterschiedlichen, vorher festgelegten Koeffizienten. Für die Implementierung im FPGA war zu beachten, dass die Auslastung im Baustein sehr hoch sein würde und deshalb mit Ressourcen sparsam umgegangen werden musste, andererseits aber auch die Verarbeitungsgeschwindigkeit ein große Rolle spielte, da nach 256ns bereits der nächste Datensatz ansteht. Somit wurden verschiedene Möglichkeiten der Realisierung überdacht bzw. an Beispielen ausgetestet 1. Aufbau von parallelen, mehrfach-genutzten 8*8 Bit Multiplikationen
aus Core Generator Elementen
Im Anschluss an die Koeffizienten-Multiplikation werden alle die Datenpakete, die über jeweils einen Multiplizierer geführt wurden, parallel-seriell gewandelt und wieder auf sechzehn Datenströme aufgeteilt, um in der nachgeschalteten FFT verarbeitet werden zu können. |
|
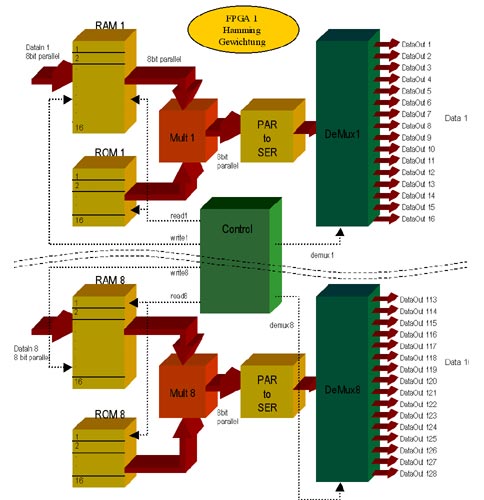 Datendecodierung und Hamming-Gewichtung |
|
| FFT Mit Hilfe einer Fourier Transformation können in einem Zeitsignal enthaltene Frequenzen ermittelt werden. Hierfür wird das Signal über einen bestimmten Zeitraum beobachtet und abgetastet. Die Abtastwerte werden gespeichert und aus diesen Daten kann das Spektrum des beobachteten Signals berechnet werden. Ein periodisches Signal mit einer Frequenz von n Hertz würde im Idealfall (gut gewählter Abtastzeitraum, keine Rundungsfehler) als Spektrum genau ein Amplitudenmaximum bei der Frequenz n aufweisen. Eine Fast Fourier Transformation (FFT) basiert auf dem Gedanken, dass durch Parallelisierung in der Bearbeitung des Zeitsignals der Rechenaufwand optimiert werden kann.
Die 128-Punkte FFT, die es zu realisieren galt, wurde völlig
modular aufgebaut, um jedes Modul für sich optimal im Hinblick
auf die Datenbreite und die benötigten Rechenoperationen beschreiben
zu können und es anschließend nur auf die benötigte
Anzahl vervielfältigen zu müssen. Die FFT besteht, wie
schon in der Einleitung erwähnt, aus sieben Stufen (128 Punkte
entspricht 2^7). Die Eingangs-Datenbreite liegt bei acht Bit –
das sind die Ergebnisse aus der Hamming-Gewichtung – und nimmt
durch die geforderte Genauigkeit in dieser Anwendung in jeder Stufe
um ein Bit zu |
|
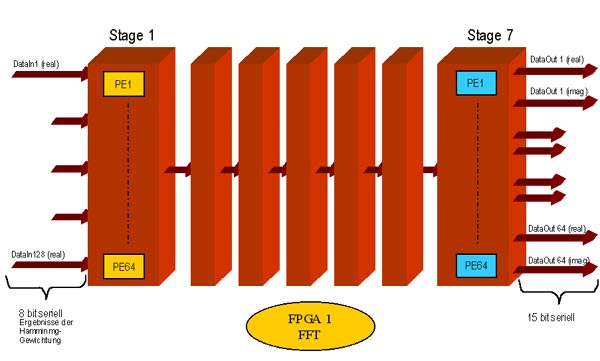 FFT bestehend aus sieben Verarbeitungsstufen |
|
Jede Stufe wiederum wird in die benötigten 64 Butterfly-PEs (PE= Prozessor Element) aufgeteilt. Unter Butterfly versteht man eine spezielle Anordnung einer PE. Zugeführt werden zwei Datenströme, wobei es sich in der ursprünglichen und damit aufwendigsten Ausbauform einer PE um komplexe Datenströme handelt. Diese Datenströme werden mit einer Komponentenform aus sin- und cos- Termen beaufschlagt. Als Ergebnis verlassen zwei meist komplexe Datenströme die Butterfly-PE. Die Berechnungen innerhalb einer PE lassen sich zurückführen auf vier reelle Multiplikationen und sechs reelle Additionen bzw. auf drei reelle Multiplikationen und sieben reelle Additionen, je nachdem, welche Berechnung besser vereinfacht werden kann. |
|
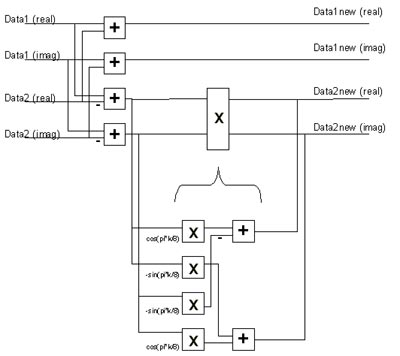 |
|
| Komplexe Butterfly-PE | |
Bei 128 Eingangsdatenströmen müssen 64 PEs pro FFT-Stufe aufgebaut werden. Die Daten sind über die gesamte FFT hinweg im Zweier-Komplement zu halten. Zur Vereinfachung der gesamten Struktur ist zu überlegen, welche Reduzierungen innerhalb der jeweiligen PEs durchgeführt werden können. In der ersten Stufe beispielsweise liegen noch keine komplexen Daten vor, d.h. die Imaginär-Zweige innerhalb der PE können ignoriert werden. Desweiteren sind die Ergebnisse der Multiplikationen mit Sinus- und Cosinuswerte von bestimmten Winkeln recht einfach zu bestimmen und benötigen nicht den gesamten Ausbausatz einer Butterfly-PE. Für den Aufbau einer komplexen PE wurden, wie auch bei der Hamming-Gewichtung, wieder verschiedene Lösungsmöglichkeiten ausgetestet und bewertet. Als Realisierung der Multiplikationen kamen im Prinzip die Ansätze aus dem vorherigen Kapitel in Betracht. Die Möglichkeiten für die Additionen waren einfach zu finden, nämlich seriell oder parallel, je nach Art der vorangegangenen Multiplikationen. Es zeigte sich, dass nur die Verwendung der seriellen Multiplikation zum gewünschten Ergebnis führen konnte, da alle anderen Möglichkeiten das FPGA zu weit mehr als 100% ausgelastet hätten. Die Multiplikation mit zunehmender Bitbreite wird immerhin viele 100 Mal durchgeführt. Eine serielle Multiplikation mit Zweier-Komplement Zahlen ist wie folgt aufgebaut: pro Rechenoperation werden jeweils zwei Multiplikationen und die angehängte Addition bzw. Subtraktion zusammengefasst (vgl. Bild oben). Folglich ergeben sich also folgende zwei Terme (die Vorzeichen sind hierbei mit beachtet):
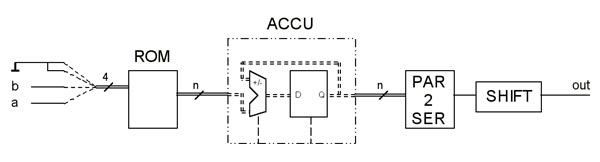
und wobei x und y für jede PE als Konstante zu sehen sind, a und b kennzeichnen die zu multiplizierenden Daten. Wird nun der erste Term genauer untersucht, so ergeben sich, wenn man sich vorstellt, dass a und b jeweils nur die Werte ’0’ oder ’1’ annehmen können, vier mögliche Ergebnisse: 0, -sin(y), cos(x) und cos(x) –sin(y). Diese Werte werden in ROMs abgelegt und mit der Adresse, die aus der Zusammenfassung der Datenströme a und b gebildet wird, adressiert. Die Ausgänge der ROMs müssen nun aufakkumuliert werden, da für eine 8-bit serielle Multiplikation die ROM-Tabelle acht mal adressiert werden muß. Hierzu wird der konfigurierbare Akkumulator aus dem Xilinx Core Generator verwendet. Dabei ist ganz speziell darauf zu achten, dass wegen der Zweier-Komplement-Darstellung der Werte, das höchstwertige Bit des Datums nicht aufaddiert sondern subtrahiert werden muss. Bei der Ansteuerung des Akkumulators muss zusätzlich beachtet werden, dass nach jedem Akkumulationsdurchlauf der Inhalt zu löschen ist, da sonst beim nächsten Durchlauf schon ein falscher Initialwert vorhanden ist. Ausgangsseitig sind die Ergebnisse nun leider parallel vorhanden und müssen im Anschluss daran wieder parallel-seriell gewandelt werden. Es fehlt noch die Anpassung an den Verarbeitungszyklus, denn da sich der Datensatz alle 256 ns erneuert, ist es sinnvoll, diesen Rahmen durch die Stufen hindurch aufrecht zu erhalten. Dies geschieht durch den Einsatz der sehr flächengünstigen SRLs (Shift Register LUT). SRLs sind keine neuen Komponenten, sondern einfach eine alternative Beschaltung innerhalb der Look-Up-Tables in den CLBs. Sie können, neben vielerlei komplexerer Funktionen, ein Schieberegister von einer Länge bis zu 16 in einem Funktionsgenerator abbilden und sind damit sehr platzsparend. Die Schieberegister werden von FFT-Stufe zu FFT-Stufe immer kürzer, da die relevanten Daten des seriellen Datenstroms mit jeder Stufe um ein Bit mehr werden und damit der Durchlauf durch den Funktionsteil immer länger dauert. Da die letzte Stufe 15 Bit breit ist, reicht die Zeit jedoch aus. |
|
 |
|
| Serielle Multiplikation | |
| Betragsbildung Ein Betrag aus einer komplexen Zahl wird normalerweise gebildet, indem man den Realteil und den Imaginärteil jeweils quadriert, die beiden Quadrate addiert und aus dem Ergebnis die Quadratwurzel zieht. Da die Beträge in diesem Fall jedoch nur für eine Größensortierung verwendet werden, kann auf das Radizieren verzichtet werden. Quadrieren an dieser Stelle bedeutet aber, dass zwei 15 Bit große Werte mit sich selbst multipliziert werden müssen. Da die Betragsbildung aus den Ergebnissen der FFT durchgeführt wird, muss diese Berechnung 64 mal stattfinden. Somit ergeben sich 128 15*15 Bit Multiplikationen und 64 31 Bit Additionen. Die verschiedenen Möglichkeiten der Realisierung führten zu keinem Ergebnis, das im verwendeten Baustein Platz gefunden hätte und dabei auch noch die Verarbeitungszykluszeit eingehalten hätte. Damit konnte diese Art der Betragsbildung nicht umgesetzt werden. Es musste mit einer Näherungsformel weitergearbeitet werden, was glücklicherweise aus Systemsicht das Ergebnis nicht zu sehr beeinträchtigt. Für diesen Näherungswert wird der Imaginäranteil mit dem Realanteil der komplexen Zahl verglichen und zu dem größeren der beiden die Hälfte des kleineren Wertes hinzuaddiert. Der größte Fehler bei dieser Näherung tritt auf, wenn beide Anteile gleich groß sind. In der praktischen Umsetzung müssen die seriellen Daten aus der FFT, zuerst seriell-parallel gewandelt werden. Anschließend ist zu prüfen, ob es sich bei den Daten um negative Werte handelt. Ist dies der Fall, so muss eine Zweier-Komplement-Bildung durchgeführt werden, da für die Betragsbildung nur die positiven Werte Verwendung finden. Zweier-Komplement-Bildung bedeutet, dass alle Bits invertiert werden und anschließend der Wert ‚1’ aufaddiert wird. Dies wird realisiert, indem in einer Schleife alle Bits mit dem Vorzeichenbit XOR-verknüpft werden. Ist das Vorzeichenbit ‚0’, so bleibt der ursprüngliche Wert erhalten, ist er ‚1’ so wird er invertiert. Nun muss nur noch zum Ergebnis das Vorzeichenbit addiert werden und schon erhält man die in Hardware kleinstmögliche Realisierung der Zweier-Komplement-Bildung. Der Vergleich der beiden positiven Werte, die Halbierung des kleineren Wertes durch einfaches Verschieben um ein Bit nach rechts und die Addition der beiden Werte sind in VHDL so beschrieben worden, dass sie vom Synthesetool als solches erkannt wurden und durch entsprechende Softmacros ersetzt werden konnten.
Sortierer Aufgabe des Sortierers ist es, die Ergebnisse aus der Betragsbildung der Größe nach zu sortieren. Die größte Anforderung hierbei bestand darin, die 15-Bit Werte innerhalb der vorgegebenen Verarbeitungszeit von 256 ns zu ordnen, da danach bereits der nächste Datensatz ansteht. Um diese Performance zu erreichen, muss hier leider auf die doppelte Taktfrequenz von 125 MHz umgestiegen werden – mittels DLL (Delay Locked Loop) lässt sich diese ‚skew-frei’ innerhalb des FPGAs erzeugen. Da durch die Taktverdoppelung nun 32 Takte zur Verfügung stehen, konnte ein hierarchischer Vergleicherbaum für die parallel verfügbaren Daten aufgebaut werden, der immer zwei Werte miteinander vergleicht. D.h. in der ersten Stufe werden 32 Vergleiche parallel durchgeführt, in der zweiten dann 16 (das sind die Ergebnisse und damit die größeren Werte aus dem ersten Vergleich) usw. bis der letzte Vergleich dann in der sechsten Stufe, also nach sechs Taktzyklen den größten Wert hervorbringt. Innerhalb des Zeitraumes von 32 Takten lassen sich auf diese Weise die fünf größten Werte aus den 64 möglichen finden. Allerdings ist darauf zu achten, dass die jeweils gefundenen Maximalwerte für die weitere Suche maskiert werden, da sonst immer wieder der gleiche Wert gefunden würde. Da sich aus der Ausführung ergibt, dass für das Auffinden der fünf größten Werte 30 Takte benötigt werden (jeweils sechs Takte für einen Durchlauf des Vergleicherbaumes) und sich aus dem Verarbeitungsrahmen von 256 ns nur 32 Takte Zeit ergeben, kann das Ausmaskieren leider nur asynchron erfolgen. Dieser Funktionsteil führte bei der Umsetzung in die Gatter-Netzliste zu den größten Problemen, das Timing einhalten zu können – ein Verarbeitungstakt von 125 Mhz mit asynchronen Rücksetzpulsen, die noch in der Zwischenzeit durchgeführt werden müssen.
Umsetzung in Gatter Der Schnitt zwischen dem ersten und dem zweiten Virtex-1000-Baustein wurde zwischen FFT und Betragsbildung gemacht. An dieser Stelle liegen die Daten seriell an und somit sind die I/O-Kapazitäten ausreichend. Da es sich um ein sehr Core-intensives Design handelt, kam die Synthese, die die Cores nur als Black Boxes behandelt, sehr schnell zu einem Ergebnis. Es zeigte sich jedoch, dass ein automatisches Plazieren und Verdrahten in den vorgegebenen Bausteinen nicht möglich war. Der erste Baustein (also der, der die Hamming-Gewichtung und die FFT beinhaltet) ist zu 98% ausgelastet, wobei von großem Vorteil ist, dass sich die Flussrichtung der Daten sehr geradlinig verhält. Auch die Datenrichtung in der Betragsbildung im zweiten Baustein ist einfach zu erkennen, bei der Sortiererfunktion wird das Ganze schon etwas schwieriger, denn da hat ein Ergebnis wieder direkten Einfluß auf alle davor-liegenden Stufen des Vergleicherbaumes. Eine weitere Schwierigkeit beim Plazieren der Komponenten im FPGA und vor allem beim Verdrahten ist die Tatsache, daß das zweite FPGA noch einige Zusatzfunktionen hat, die u.a. alle Block-RAMs benötigen und damit viele Netze mit hohem Fanout von zentraler Stelle bis an die Bausteinkanten (wo die Block-RAMs plaziert sind) geführt werden müssen. Durch Duplizierung der bildenden Funktionen für diese Netze konnte die Problematik in den Griff bekommen werden. Bei beiden Bausteinen musste die gesamte Struktur durch manuelles Plazieren erzeugt werden, was sich als sehr aufwändig herausstellte. Es war sogar notwendig, die vorgegebenen Plazierungsmakros bestimmter Core-Elemente zu ändern, um sie enger an andere Elemente schieben zu können. Mit Hilfe der erzeugten Floorplan-Dateien liefen die Xilinx-Backend-Tools jedoch recht schnell über das Design und brachten das gewünschte Ergebnis, das durch Statische Timinganalyse und geeignete Timingsimulation schließlich noch verifiziert wurde.
Fazit und Ausblick Zum Abschluss der teilweise sehr genauen Ausführungen ist anzumerken, daß sich bei dieser Anwendung mit Sicherheit der Aufwand gelohnt hat, die möglichen Lösungsansätze an kleinen Beispielen im Hinblick auf Timing und Ressourcen durchzutesten und hochzurechnen, denn ohne diese strukturierte und detaillierte Kleinarbeit wäre das gesamte Projekt an der Komplexität der Funktionen gescheitert. Das Design wurde in großem Maße optimal an die Technologie angepasst, was genaue Kenntnisse derer voraussetzt und nur dadurch, gepaart mit der immensen Ausdauer, immer neue Wege zu begehen, konnte es auch realisiert werden. In einem anderen Baustein mit anderer Technologie hätten mit Sicherheit auch ganz andere Lösungsmöglichkeiten in Betracht gezogen werden müssen. Beispielsweise, die Xilinx Baustein-Familie Virtex II genauer betrachtend - zu Beginn der Entwicklungsphase stand sie leider noch nicht zur Verfügung -, wäre eine Realisierung deutlich anders und an einigen Stellen auch wesentlich einfacher gewesen - man denke nur an die Möglichkeit der Verwendung der schon eingebauten Parallel-Multiplizierer. Aber auch für diese FPGAs wird es wieder Anwendungsfälle geben, die die Bausteine an den Rand ihrer Aufnahmekapazität bringen und genauso wieder Erfahrung und beste Kenntnisse in Tools und Technologien erfordern. |
|